El direccionamiento es una función clave de los protocolos de capa de red que permite la comunicación de datos entre hosts, independientemente de si los hosts se encuentran en la misma red o en redes diferentes. Tanto el protocolo de Internet versión 4 (IPv4) como el protocolo de Internet versión 6 (IPv6) proporcionan direccionamiento jerárquico para los paquetes que transportan datos.
El diseño, la implementación y la administración de un plan de direccionamiento IP eficaz asegura que las redes puedan operar de manera eficaz y eficiente.
En este capítulo, se examina detalladamente la estructura de las direcciones IP y su aplicación en la construcción y la puesta a prueba de redes y subredes IP.
1. Notación binaria
Para comprender el funcionamiento de los dispositivos en una red, debemos observar las direcciones y otros datos de la misma manera en que lo hacen los dispositivos: en notación binaria.
La notación binaria es una representación de la información mediante unos y ceros solamente. Las PC se comunican mediante datos binarios. Los datos binarios se pueden utilizar para representar muchas formas distintas de datos. Por ejemplo, al pulsar letras en un teclado, esas letras aparecen en la pantalla de una manera que el usuario puede leer y comprender. Sin embargo, la PC traduce cada letra a una serie de dígitos binarios para su almacenamiento y transporte. Para traducir esas letras, la PC utiliza el Código Estadounidense Estándar para el Intercambio de Información (ASCII).
Mediante ASCII, la letra “A” se representa en forma de bit como “01000001”, mientras que la “a” minúscula se representa en forma de bit como “01100001”. Utilice el traductor de ASCII en la figura 1 para convertir los caracteres ASCII al sistema binario.
Si bien, por lo general, las personas no deben preocuparse por la conversión binaria de letras, es necesario comprender el uso del sistema binario para el direccionamiento IP. Cada dispositivo en una red se debe identificar de forma exclusiva mediante una dirección binaria. En redes IPv4, esta dirección se representa mediante una cadena de 32 bits (unos y ceros). A continuación, en la capa de red, los paquetes incluyen esta información de identificación única para los sistemas de origen y de destino. Por lo tanto, en una red IPv4, cada paquete incluye una dirección de origen de 32 bits y una dirección de destino de 32 bits en el encabezado de capa 3.
Para la mayoría de las personas, una cadena de 32 bits es difícil de interpretar e incluso más difícil de recordar. Por este motivo, representamos las direcciones IPv4 mediante el formato decimal punteado en lugar del binario.
Esto significa que vemos a cada byte (octeto) como número decimal en el rango de 0 a 255. Para entender cómo funciona esto, es necesario tener aptitudes para la conversión de sistema binario a decimal.
Notación de posición
Aprender a convertir el sistema binario a decimal requiere el conocimiento de los fundamentos matemáticos de un sistema de numeración denominado notación de posición. “Notación de posición” significa que un dígito representa diferentes valores según la posición que ocupa. En un sistema de notación de posición, la base numérica se denomina “raíz”. En el sistema de base 10, la raíz es 10. En el sistema binario, se utiliza una raíz de 2. Los términos “raíz” y “base” se pueden utilizar de manera indistinta. Más específicamente, el valor que un dígito representa es el valor multiplicado por la potencia de la base o raíz representado por la posición que el dígito ocupa. Algunos ejemplo ayudarán a aclarar cómo funciona este sistema.
Para el número decimal 192, el valor que el 1 representa es 1*10^2 (1 multiplicado por 10 elevado a la segunda potencia). El 1 se encuentra en lo que comúnmente llamamos la posición "100". La notación de posición se refiere a esta posición como posición base^2 porque la base o raíz es 10 y la potencia es 2. El 9 representa 9*10^1 (9 multiplicado por 10 elevado a la primera potencia). En la figura 2, se muestra la notación de posición para el número decimal 192.
Usando la notación de posición en el sistema de numeración con base 10, 192 representa:
192 = (1 * 10^2) + (9 * 10^1) + (2 * 10^0)
o
192 = (1 * 100) + (9 * 10) + (2 * 1)
2. Sistema de numeración binario
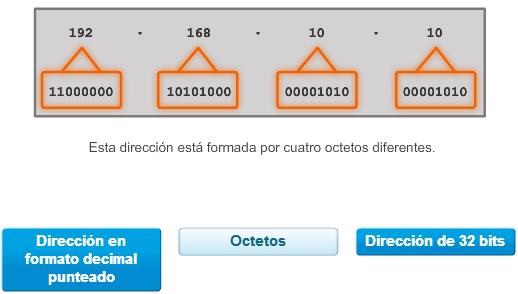
En IPv4, las direcciones son números binarios de 32 bits. Sin embargo, para facilitar el uso por parte de las personas, los patrones binarios que representan direcciones IPv4 se expresan en formato decimal punteado. Esto primero se logra separando cada byte (8 bits) del patrón binario de 32 bits, llamado “octeto”, con un punto. Se le llama octeto debido a que cada número decimal representa un byte u 8 bits.
La dirección binaria:
11000000 10101000 00001010 00001010
se expresa como decimal punteada de la siguiente manera:
192.168.10.10
En la figura 1, seleccione cada botón para ver cómo se representa la dirección binaria de 32 bits en octetos decimales punteados.
¿Pero de qué forma se determinan los equivalentes decimales reales?
Sistema de numeración binaria
En el sistema de numeración binaria la raíz es 2. Por lo tanto, cada posición representa aumentos en potencias de 2. En números binarios de 8 bits, las posiciones representan estas cantidades:
2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0
128 64 32 16 8 4 2 1
El sistema de numeración de base 2 solo tiene dos dígitos: 0 y 1.
Cuando se interpreta un byte como un número decimal, se obtiene la cantidad que esa posición representa si el dígito es 1, y no se obtiene la cantidad si el dígito es 0, como se muestra en la figura 1.
En la figura 2, se ilustra la representación del número decimal 192 en sistema binario. Un 1 en una determinada posición significa que se agrega ese valor al total. Un 0 significa que no se agrega ese valor. El número binario 11000000 tiene un 1 en la posición 2^7 (valor decimal 128) y un 1 en la posición 2^6 (valor decimal 64). Los bits restantes son todos 0, de modo que no se agregan los valores decimales correspondientes. El resultado de agregar 128 + 64 es 192, el equivalente decimal de 11000000.
A continuación, se proporcionan dos ejemplos más:
Ejemplo 1: un octeto compuesto solo por unos, 11111111
Un 1 en cada posición significa que sumamos el valor para esa posición al total. Todos 1 significa que se incluyen los valores de cada posición en el total; por lo tanto, el valor de todos 1 en un octeto es 255.
128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
Ejemplo 2: un octeto compuesto solo por ceros, 00000000
Un 0 en cada posición indica que no se incluye el valor para esa posición en el total. Un 0 en cada posición produce un total de 0.
0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
Una combinación distinta de unos y ceros arroja un valor decimal diferente.
Figura 1
Espero haber ayudado en algo. Hasta la próxima oportunidad!
Twittear





No hay comentarios:
Publicar un comentario