Los problemas de optimización lineal con apenas dos variables de decisión, pueden ser resueltos gráficamente, en esta sección mostraremos los pasos a seguir, para encontrar la solución de un problema lineal de dos variables.
Paso 1: Construcción de la región factible
En primer lugar trazamos los ejes coordenados con las variables x1 y x2 . Ahora para poder graficar los semiplanos correspondientes a cada restricción, debemos convertir las desigualdades en igualdades, porque la representación gráfica de una ecuación lineal con dos variables es una recta y graficarla es simple. Por tal motivo graficamos las rectas correspondientes a cada una de las restricciones del problema y después seleccionaremos el semiplano correspondiente a cada desigualdad.
La primera restricción del problema es 9x1 + x2 <= 18 , cuya representación geométrica es un semiplano. En primer lugar graficamos la recta 9x1 + x2 = 8, para este fin tabulamos dos puntos por donde debe pasar la recta, más aún si necesitamos saber en qué puntos corta la recta a los ejes coordenados, sólo debemos asignar el valor de cero a cada una de las variables, del siguiente modo:
Si x1 = 0 al sustituir en la ecuación de la recta tenemos 9(0) + x2 = 18 , entonces x2 = 18 .
Por tanto, tenemos el punto (x1, x2) = (0,18).
De forma similar, si x2 = 0 al sustituir en la ecuación de la recta tenemos 9x1 + (0) = 18 , entonces x1 = 2. Por tanto, tenemos el punto (x1, x2 )= (2,0).
Finalmente podemos graficar la recta 9x1 + x2 = 18
Para poder determinar el semiplano correspondiente a la desigualdad 9x1 + x2 = 18, seleccionamos un punto (x1, x2) arbitrario, en este caso seleccionamos el punto (1,1) ubicado por debajo de la recta 9x1 + x2 = 18, a continuación verificamos si éste punto seleccionado cumple con la desigualdad: 9(1) + 1 = 10 <= 18 , podemos ver que cumple con la desigualdad y dado que el punto seleccionado (1,1) está ubicado por debajo de la recta, entonces el semiplano correspondiente a la restricción está por debajo de la recta tal como se muestra en la Figura 2
De manera similar determinamos el semiplano correspondiente a la segunda restricción 3x1 + x2 <= 12. Para esto debemos tabular dos puntos para graficar la recta 3x1 + x2 = 12 y al seleccionar el punto (1,1), podemos ver que dicho punto cumple con la desigualdad:
3(1) + 1 = 4 <= 12 y como este punto (1,1) está ubicado por debajo de la recta, entonces el semiplano correspondiente a la restricción está por debajo de la recta 3x1 + x2 = 12 tal como se muestra en la Figura 3
Las restricciones de no negatividad, x1 >= 0 , x2 >= 0 gráficamente corresponde al primer cuadrante del plano cartesiano.
Finalmente para determinar la región factible debemos interceptar los semiplanos de las restricciones respectivas.
Paso 2: Determinación de la solución optima.
En primer lugar debemos graficar la recta que corresponde a la función objetivo que pasa por un punto (x1, x2) perteneciente a la región factible.
Sea
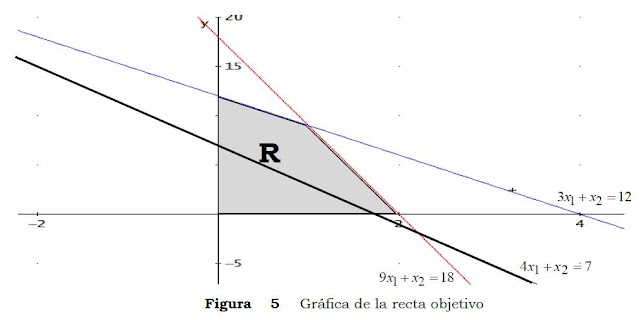
, calculamos el valor de z = 4(1) + 3 = 7, este valor nos permite construir la recta 4x1 + x2 = 7 que pasa por el punto (x1, x2) = (1,3). Esta recta es secante a la región factible, como se puede observar en la Figura 5
, calculamos el valor de z = 4(1) + 3 = 7, este valor nos permite construir la recta 4x1 + x2 = 7 que pasa por el punto (x1, x2) = (1,3). Esta recta es secante a la región factible, como se puede observar en la Figura 5
Por otro lado debemos determinar la dirección en la que la recta objetivo aumenta su valor, para esto utilizamos el gradiente de la función objetivo, dado que este vector indica la dirección de crecimiento de una función de varias variables. Por tal motivo es de suma importancia conocer la dirección del vector gradiente de la función objetivo.
Podemos determinar el gradiente de la función del siguiente modo
Este vector gradiente es perpendicular a la recta 4x1 + x2 = 7 y a partir de allí nos desplazaremos paralelamente siguiendo la dirección del vector gradiente, hasta que la recta objetivo sea tangente a la región factible.
En efecto, siendo z = 4x1 + x2 la función objetivo, obtenemos su vector gradiente
y desplazamos la recta objetivo siguiendo la dirección del vector gradiente hasta tornarse tangente a la región factible, obteniendo el punto óptimo del problema de optimización lineal.
y desplazamos la recta objetivo siguiendo la dirección del vector gradiente hasta tornarse tangente a la región factible, obteniendo el punto óptimo del problema de optimización lineal.
Por tanto, si fabricamos x1 =1 Ben 10 y x2 = 9 DinoRey, tendremos una utilidad máxima de 13 dólares. Al sustituir el valor de las variables de decisión en cada una de las restricciones, tenemos:
(Disponibilidad de sensores electrónicos) 9(1)+9=18
(Disponibilidad de mano de obra) 3(1)+9=12
Por tanto podemos afirmar que se utilizaron todos los sensores electrónicos así como toda la mano de obra. Esto nos permite introducir los siguientes conceptos de restricción saturada y no saturada.
Definición 4. Una restricción es activa (saturada), si al sustituir los valores óptimos de la variable de decisión el primer y segundo miembro de la restricción son iguales.
Definición 5. Una restricción es inactiva (no saturada), si al sustituir los valores óptimos de la variable de decisión el primer y segundo miembro de la restricción son diferentes.
Observaciones:
- En la Figura 6, podemos ver que el punto óptimo está ubicado en la intersección de las restricciones saturadas.
- Para el caso de un problema de minimización debemos seguir la dirección del gradiente negativo.
Espero haber ayudado en algo. Hasta la próxima oportunidad!
Twittear










Todo esto lo tuve que volver a cursar por no entenderlo en la clase de ahorros para el retiro que aun no puedo olvidar
ResponderEliminarHola Cain Velazquez, gracias por participar. Saludos!
Eliminar